Duke Mathematics Has Its Day in Court

DURHAM, N.C. -- On March 26, the U.S. Supreme Court is set to hear a North Carolina lawsuit that could end partisan gerrymandering for good -- and a mode of analysis developed at Duke University could impact their decision.

The nation’s highest court may finally weigh in on the practice of manipulating political district boundaries to favor one party at the expense of another. A key issue in the case, Rucho v. Common Cause, is whether the 2016 North Carolina congressional plan violates the First Amendment by diluting the influence of some voters based on their political affiliations.

This isn’t the first time a partisan gerrymandering challenge to the state’s legislative maps has made it to the Supreme Court. Last year the court sidestepped the issue, sending the case back to the lower court without issuing a decisive ruling. Part of the reason, the justices said, was the lack of a clear standard by which to gauge which gerrymanders go too far.

Now the case is back before the court on appeal, and Duke mathematicians say they have a way to determine, in specific districts, when a map is suspicious. In expert witness testimony cited in an appellee’s brief for the case, math professor Jonathan Mattingly showed results from a computer sampling method his team developed to tell when a map tilts too far to one party or another.

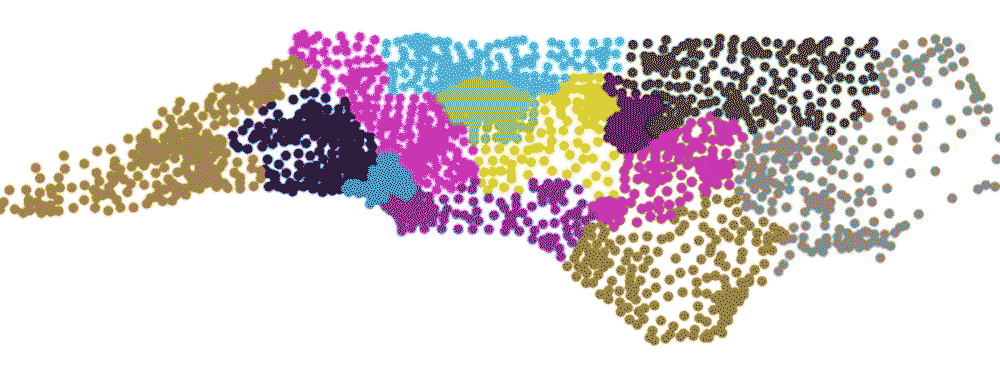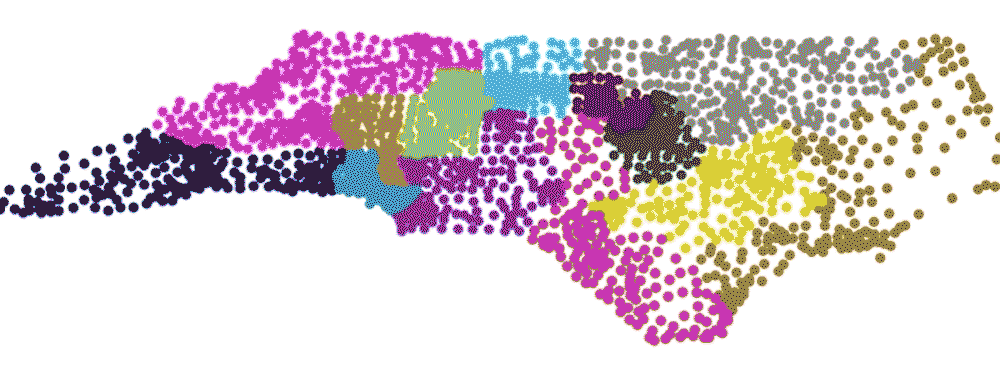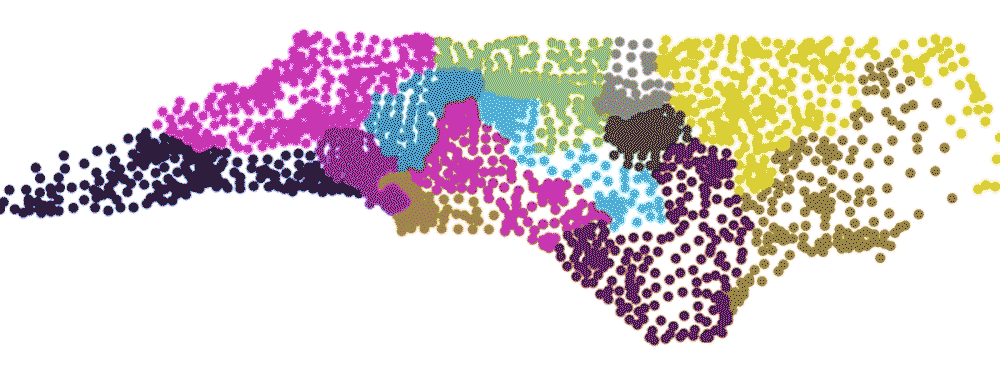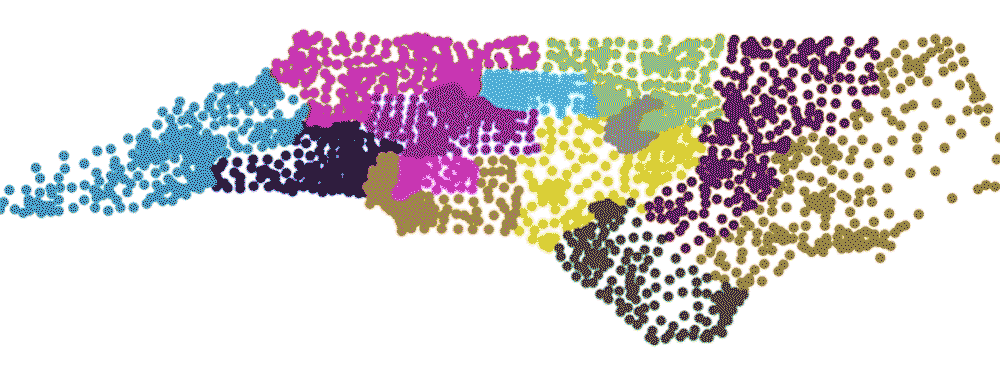
Their method assesses how the outcome of an election would have differed had comparable, but more neutral maps been used. With help from assistant research professor Gregory Herschlag, the team used computer algorithms to generate more than 24,000 alternative maps that meet the state’s redistricting criteria, without regard to party affiliation. Then, using the actual vote tallies from each precinct, they did a simulation to see what would happen if they re-ran the election under each map.

By varying how the districts are drawn, and without changing a single vote, the team’s simulations showed it is possible to sway the outcome of a congressional election in North Carolina by as many as five seats.

“With the exact same votes, you can end up with completely divergent outcomes,” Mattingly says.

Using actual 2016 congressional votes, fewer than one percent of the 24,000-plus maps Mattingly’s team generated yielded the 10-3 Republican advantage that North Carolina saw in the 2016 election. Democrats won just three of North Carolina’s 13 U.S. House seats in 2016, even though the votes were closely split 47-53 percent between the two major parties. None of the 24,000 theoretical maps could give Democrats fewer than three seats.

In other words, Mattingly says, the General Assembly could not have drawn a map that turned the close statewide vote totals into more lopsided results if they tried.

The researchers also ran their analyses across different elections. They found that the state’s map ensures that Republicans keep their 10:3 edge even if their share of the vote starts to drop. The vast majority of the theoretical maps failed to maintain Republican control of that many seats.

“We call this the firewall effect,” Mattingly says.

Since congressional district lines are redrawn every 10 years, this firewall effect would continue to insulate Republicans against all but the biggest “blue wave,” entrenching them in power for a least a decade.

Mattingly’s simulations also show which specific districts were engineered to marginalize the minority party. To do this, he plotted the Democratic vote share for each of NC’s 13 districts on a graph, and ordered the districts left to right, from most Republican to most Democratic.

Most neutral maps yield a straight line: As more people cast votes for one party, the number of districts that flip to that party grows steadily.

But the 2016 map is different. A district-by-district tally of the actual results for the 2016 map plotted on a graph resembles an “S.” Democratic voters at the top of the “S” are crammed into a handful of districts with other like-minded voters, where they get a few overwhelming wins. And Democratic voters at the bottom are divided across several districts so they have a harder time winning a majority in any district.

Lawyers arguing against the current North Carolina map call this S-shaped curve the “signature of gerrymandering.”

The researchers showed that the packing and cracking in certain districts in the 2016 map was more extreme than in more than 99 percent of other maps the state could have chosen.

”I’m not advocating that we use computers to draw our maps,” Mattingly says. “But I think we can use them to say whether a map is beyond the pale.”

Without such tests for statistical outliers, it’s not as simple as you might think to spot a gerrymandered map, Mattingly says. Disproportionate results may be a red flag, but they’re no smoking gun. Democratic clustering in cities means fewer districts are able to build Democratic majorities. Even without partisan gerrymandering, Democrats can win 50 percent of the vote and still capture fewer than 50 percent of House seats.

You can’t tell a gerrymandered map by its shape, either, Mattingly says. Some of North Carolina’s funkier-looking congressional districts have been compared to a snake, or an octopus, or a mutant crab. Mattingly tested North Carolina's oddly shaped 2012 congressional map, which was struck down and replaced with a more pleasing-looking map in 2016. The redrawn version gave results that were just as atypical as its bizarre-looking predecessor.

The North Carolina lawsuit is one of two partisan gerrymandering challenges the Supreme Court is expected to hear March 26. In the other case, Lamone v. Benisek, the question is whether Maryland violated the First Amendment in drawing lines to favor Democrats.

Though Duke researchers were not expert witnesses in the Lamone case, Duke statistical science graduate student Lisa Lebovici analyzed the 2011 Maryland congressional map using similar methods.

She found that while many other maps would have ultimately produced the same 7-1 victory seen in 2012, the 2011 plan made the race for the contentious seventh seat less competitive than it arguably should have been according to multiple simulations.

A decision on both cases is expected by this summer.